The MABIA method requires data on water holding capacity at field capacity and wilt point, for each catchment land use. Because direct measurement of a soil's water holding capacity, including saturation, field capacity and wilt point, can be costly and time consuming, pedotransfer functions were developed to translate more easily obtainable data into these water holding capacity values. The SoilProfiles function estimates average soil water capacity (saturation, field capacity and wilt point) using one of six available pedotransfer functions (PTF), in order to determine the Soil Water Capacity for catchment land use branches. This function can average over several soil profiles (sampling sites) and soil horizons (layers). (As an alternative to using SoilProfiles, you can enter field capacity and wilt point directly, or choose a texture class from the Soil Library.)
If using two buckets for the MABIA water balance calculation, WEAP will calculate the average soil water capacity separately for the top and bottom bucket, based on the horizons that fall within each bucket. The size of the buckets changes as the rooting depth changes. If not using two buckets, the average soil water capacity will be calculated from all horizons.
If there are multiple profiles (sampling sites), the average field capacity and wilt point over all the profiles is the simple average over all the profiles:
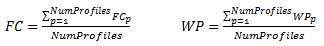
where
FC = field capacity averaged over all profiles
FCp = average field capacity
for profile p,
WP = wilt point averaged over all profiles
WPp = average wilt point for
profile p,
NumProfiles = number of profiles to average
If there are multiple horizons (layers) in a profile, the average field capacity and wilt point for the profile is the weighted average over the horizons in each bucket (two bucket method) or all horizons (one bucket method). The weighting is by horizon thickness:
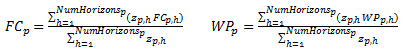
where
FCp
= average field capacity for profile p,
FCp,h = field capacity of horizon
h in profile p,
WPp = average wilt point for
profile p,
WPp,h = wilt point of horizon
h in profile p,
NumHorizonsp = number of horizons
in profile p,
zp,h = thickness of horizon h
in profile p
The presence of coarse fragments (e.g., rocks) will reduce the water hold capacity of the soil.
FC'p,h = FCp,h * (1 - CFp,h) WP'p,h = WPp,h * (1 - CFp,h)
where
FC'p,h = field capacity of horizon h
in profile p, corrected for coarse fragments,
FCp,h = field capacity of horizon
h in profile p,
WP'p,h
= wilt point of horizon h in profile p, corrected for coarse fragments,
WPp,h = wilt point of horizon
h in profile p,
CFp,h = coarse fragment fraction
of horizon h in profile p
Field capacity and wilt point for each horizon in each profile are estimated using pedotransfer functions. The pedotransfer functions are commonly categorized into “class” and “continuous” PTFs, based on the parameters to use in estimating the water content. The “class” PTFs are defined based on the soil texture class to which the soil sample belongs, while the "continuous" PTFs predict the soil properties as a continuous function of one or more measured variables. This latter type of pedotransfer function can be used either to predict the soil water content at a special point of the water retention curve or to predict the parameters of an hydraulic model. The most widely used is the Van-Genuchten hydraulic model:
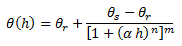
where
qr and qs are the residual and saturated water
content, respectively,
h is the matric potential (kPa), for Saturation point (h=0 kPa), Field
Capacity (h=100 kPa) and Wilting Point (h=1500 kPa)
a is the scaling parameter,
n is the curve shape factor,
m is an empirical constant, which can be related to n, by m = 1 – 1/n.
Six continuous pedotransfer functions are available in the MABIA method. They were chosen to accommodate varying data availability, in terms of which of the following were available: particle size fractions, dry bulk density and organic matter content.
"Particle size (Jabloun and Sahli 2006)": silt[%], clay[%], and sand[%] fraction
"Particle size Bulk density (Jabloun and Sahli 2006)": silt[%], clay[%], and sand[%] and bulk density[g/cm^3]
"Particle size Organic matter (Jabloun and Sahli 2006)": silt[%], clay[%], and sand[%] and organic matter[g/kg]
"Particle size Bulk density Organic matter (Jabloun and Sahli 2006)": silt[%], clay[%], and sand[%], bulk density[g/cm^3] and organic matter[g/kg]
"Particle size Bulk density Organic matter (Vereecken et. al. 1989)": silt[%], clay[%], and sand[%], bulk density[g/cm^3] and organic matter[g/kg]
"Particle size Bulk density Organic matter (Wösten et. al. 1999)": silt[%], clay[%], and sand[%], bulk density[g/cm^3] and organic matter[g/kg]
In the following equations,
Cl = Clay [%]
Si = Silt [%]
Sa = Sand [%] = 100% - Cl - Si
BD = Bulk density [g/cm^3]
OM = Organic matter [g/kg]
This model is defined by three specific equations to estimate water content at saturation, field capacity and wilting point.
qSAT = 0.6658(Si) + 0.1567(Sa) - 0.0079(Si^2)
- 12.31121/Sa
- 6.4756
Ln(Sa) - 0.0038(Cl)(Si) + 0.0038(Cl)(Sa) - 0.0042(Si)(Sa) + 52.7526
qFC =
118.932(Cl) + 119.0866(Si) + 119.1104(Sa) + 162.31731/Cl -
46.21921/Si-5.12991/Sa
+ 18.1733
Ln(Cl) + 0.0013(Cl)(Si) + 0.0022(Si)(Sa) - 11939.3493
qWP =
-1.5722(Si) - 0.5423(Sa) - 0.0072(Cl^2) + 0.0072(Si^2)
- 0.0059(Sa^2)
+ 160.14591/Cl
+ 6.60011/Sa
+ 0.0022(Cl)(Si)
- 0.0039(Cl)(Sa) + 92.3851
This model is defined by three specific equations to estimate water content at saturation, field capacity and wilting point.
qSAT = 0.4602(Cl) + 1.1343(Si) - 86.8963(BD)
- 0.011(Si^2) -
9.4193 Ln(Si) + 110.5222 Ln(BD) - 0.256(Cl)BD - 0.002(Si)(Sa) + 0.0405(Sa)(BD)
+ 135.5837
qFC =
148.39031/Cl
- 43.85161/Si
- 5.17411/Sa
+ 16.6718
Ln(Cl) + 0.0011(Cl)(Si) - 0.0999(Cl)(BD) +
0.0025(Si)(Sa) - 24.1522
qWP =
-1.2152(Si) - 0.4877(Sa) - 0.0057(Cl^2) +
0.0087(Si^2) +
85.84361/Cl
- 88.0331/Si
+ 0.0012(Cl)(Si)
+ 0.2129(Cl)(BD) +
59.6137
This model is defined by three specific equations to estimate water content at saturation, field capacity and wilting point.
qSAT = 0.7264(Si) + 0.2026(Sa) - 0.0083(Si^2)
- 13.75491/Sa
- 7.7387
Ln(Sa) + 2.2103 Ln(OM) - 0.0043(Cl)(Si) + 0.0051(Cl)(Sa) - 0.0047(Si)(Sa)
+ 53.4646
qFC =
0.2239(Cl) - 57.95441/Si -
11.69741/Sa
+ 6.90031/OM
- 3.5324
Ln(Sa) + 24.0966 Ln(OM) + 0.0031(Cl)(Sa) - 0.1886(Cl)(OM) + 36.7918
qWP =
-181.7238(Cl) - 183.5092(Si) - 182.4525(Sa) - 0.0048(Cl^2) +
0.0114(Si^2) -
0.0031(Sa^2) +
128.78961/Cl
- 83.0451/Si
+ 6.52931/Sa
+ 9.18951/OM
+ 27.4919
Ln(OM) + 0.0043(Cl)(Si) - 0.2411
This model is defined by three specific equations to estimate water content at saturation, field capacity and wilting point.
qSAT= -0.8667(Cl) - 1.426(Sa) - 84.2817(BD)
- 0.0151(Si^2) +
0.0012(Sa^2) -
7.9188 Ln(Si) + 112.0333 Ln(BD) - 0.0064(Cl)(Si) - 0.2835(Cl)(BD) - 0.0068(Si)(Sa)
+ 0.177(Si)(OM) + 266.768
qFC =
0.0023(Si^2) -
8.491(BD^2) -
3.2498(OM^2) +
153.59021/Cl
- 101.21431/Si-9.02181/Sa +
8.52011/OM
+ 20.9002
Ln(OM) + 0.355(Cl)(BD) - 0.2388(Cl)(OM) + 10.1357(BD)(OM) + 16.4788
qWP =
-0.7409(Si) + 0.0126(Si^2) -
7.4396(BD^2) -
2.8807(OM^2) + 136.151/Cl -
98.33231/Si
- 23.99671/Sa
+ 9.03681/OM
+ 20.7999
Ln(OM) + 0.4598(Cl)(BD) - 0.2579(Cl)(OM) + 9.1905(BD)(OM) + 9.8444
The water content at saturation, field capacity and wilting point are obtained by calculating the Van-Genuchten model for h = 0, 100 and 1500, respectively.
qSAT= qr + (qs - qr) / (1 + (a
* 0) ^ n) ^ m = qs
qFC = qr + (qs - qr) / (1 + (a
* 100) ^ n) ^ m
qWP = qr + (qs - qr) / (1 + (a
* 1500) ^ n) ^ m
where
qs =
0.81- 0.283(BD) + 0.001(Cl)
qr = 0.015+ 0.005(Cl)
+ 0.014(OM)
a = Exp( -2.486+ 0.025(S) - 0.351(OM) - 2.617(BD) - 0.023(Cl) )
n = Exp( 0.053- 0.009(S) - 0.0135(Cl) + 0.00015(S)² )
m = 1
The water content at saturation, field capacity and wilting point are obtained by calculating the Van-Genuchten model for h = 0, 100 and 1500, respectively.
qSAT= qr + (qs - qr) / (1 + (a
* 0) ^ n) ^ m = qs
qFC = qr + (qs - qr) / (1 + (a
* 100) ^ n) ^ m
qWP = qr + (qs - qr) / (1 + (a
* 1500) ^ n) ^ m
where
qs = 0.7919 + 0.001691(Cl) - 0.29619(BD)
- 0.000001491(Si^2) + 0.0000821(OM^2) + (0.02427 )/Cl+ 0.01113/Si +
0.01472 ln(Si) - 0.0000733(OM)(Cl) - 0.000619(BD)(Cl) - 0.001183(BD)(OM)
- 0.0001664(Si)
qr = 0.01
a = exp[-14.96 + 0.03135(Cl) + 0.0351(Si) + 0.646(OM) + 15.29(BD)
- 0.192 - 4.671(BD^2) - 0.000781(Cl^2) - 0.00687(OM^2) + 0.0449/OM +
0.0663 Ln(Si) + 0.1482 Ln(OM) - 0.04546(BD)(Si) - 0.4852(BD)(OM) + 0.00673(Cl)]
n = exp[-25.23 - 0.02195(Cl) + 0.0074(Si) - 0.194(OM) + 45.5(BD) - 7.24(BD^2)
+ 0.0003658(Cl^2)
+ 0.002885(OM^2) - 12.81/BD -
0.1524/Si -
0.01958/OM -
0.2876 Ln(Si) - 0.0709 Ln(OM) - 44.6 Ln(BD) - 0.02264(BD)(Cl) + 0.0896(BD)(OM)
+ 0.00718(Cl)] +
1
m = 1-1/n